May 19th, 2024
Deciphering Effect Size
By Alex Kuo · 8 min read

Overview
Effect size is a critical concept in statistics that measures the strength of the relationship between two variables. It's a tool that helps researchers understand the practical significance of their findings, beyond mere statistical significance. This blog aims to demystify effect size, explore its various types, and illustrate how tools like Julius can assist researchers in calculating and interpreting this important measure.
What is Effect Size?
Why is Effect Size Important?
Types of Effect Size
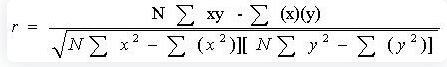
r = correlation coefficient
N = number of pairs of scores
∑xy = sum of the products of paired scores
∑x = sum of x scores
∑y = sum of y scores
∑x2= sum of squared x scores
∑y2= sum of squared y scores
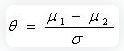
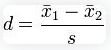
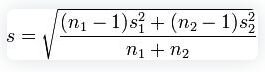
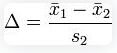
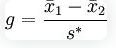
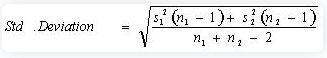
6. Cohen’s f²: Used in the context of ANOVA and multiple regression to measure the effect size based on the squared multiple correlation.

8. Odds Ratio: Used in binary data to compare the odds of success between two groups. For example, it is used if we have the following table:
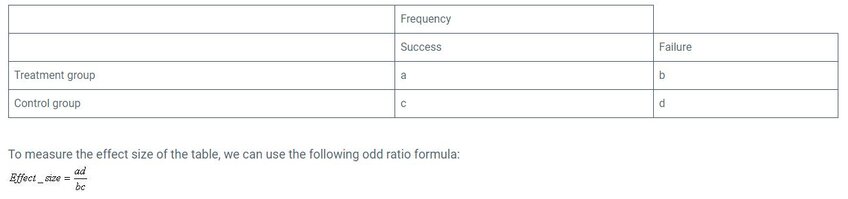
Calculating Effect Size
The Role of Julius in Calculating Effect Size
Julius can significantly enhance the process of calculating and interpreting effect size:
- Automated Calculations: Julius can automatically compute various types of effect sizes from your data, saving time and reducing errors.
- Data Visualization: It provides visual representations of effect sizes, making it easier to understand and communicate the results.
- Interpretation Guidance: Julius offers guidance on interpreting the effect sizes, helping you understand what the numbers actually mean for your research.
- Comparative Analysis: It can compare effect sizes across different studies or groups, providing a broader context for your findings.
Conclusion
Effect size is a fundamental concept in statistics that provides deep insights into the practical significance of research findings. Understanding and accurately calculating effect size is crucial for researchers across various disciplines. Tools like Julius can provide invaluable assistance, making the process more efficient and the results more interpretable. Whether you're a seasoned researcher or a student just starting out, mastering the concept of effect size will significantly enhance your analytical capabilities and help you make more informed conclusions from your data.
